SPATIAL STATISTICS (STATISTIK SPATIAL)
Statistik Spatial
§
Statistik Centrographic
tunggal, langkah-langkah ringkas dari distribusi
spasial
§
Analisis Pola titik
Analisis pola; poin tidak memiliki besaran (“bukan
variabel”)
Analisis Quadrat
Analisis Tetangga Terdekat
§
Autokorelasi Spatial
- Satu
valiabel
Matrik bobot
Statistik Hitungan Gabungan
Moran’s I
Geary’s C Ratio
General G
LISA
§
Korelasi dan Regresi
- Dua
variabel
Standard [ Y = a + bx ]
Spatial
Statistik
Deskripsi
§
Statistik deskripsi dan penjelasan deskripsi
Berkaitan dengan memperoleh ringkasan pengukuran untuk
menggambarkan seperangkat data.
§
Statistik kesimpulan dan statistik dapat disimpulkan
Berkaitan dengan membuat kesimpulan dari sampel
tentang populasi.
Berkaitan dengan membuat kesimpulan yang sah
tentang mendasari proses dari pola yang diamati.
§ Statistik
non parametrik → data didasarkan pada pengamatan/observasi
Ulangan (r) non parametrik lebih banyak daripada
ulangan parametrik
1.
Statistik Deskriptif Klasik : Univariate
(satu variable)
1.1 Ukuran Pemusatan dan Dispersi
§
Pusat Tendensi merupakan salah satu teknik
analisis data dalam statistik deskripsi. Tendensi merupakan angka yang menjadi
ukuran dari pemusatan distribusi data.
Ringkasan untuk ukuran satu variable tunggal :
- Mean (rerata)
- Median (nilai tengah)
- Mode (yang paling sering muncul)
Distribusi data dapat dikatakan baik ketika data
berdistribusi normal. Nilai dari mean, median dan modus juga akan berpengaruh
terhadap kurva distribusi data yang terbentuk.
· Ketika nilai mean, median dan modus saling berhimpit, maka akan
membentuk kurva distribusi normal.
· Ketika nilai mean lebih besar dari nilai median dan modus, maka akan
membentuk kurva landai ke kanan (+)
· Ketika nilai mean lebih kecil dari nilai median dan modus, maka akan
membentuk kurva landai ke kiri (-)
§
Dispersi: ukuran sebaran atau variabilitas
- Variance (variasi)
- Simpangan baku (akar kuadrat dari variasi)
Pusat
tendensi bisa didapat dalam ArcGIS dengan:
- Membuka
sebuah table, klik kanan mouse pada heading kolom dan pilih Statistics.
- Pergi
ke ArcToolbox>Analysis>Statistics>Summary Statistics
1.2 Distribusi
Frekuensi
Sebuah
penghitungan frekuensi yang nilainya terjadi pada variabel
§
Paling mudah dipahami untuk variabel kategori
(e.g. kesukuan)
§
Untuk variable kontinu, frekuensi dapat di :
- Dihitung dengan membagi variable ke dalam kategori
atau “keranjang” (e.g kelompok masukan)
- Digambarkan oleh proporsi luasan dibawah kurva
frekuensi
Dalam ArcGIS, kita dapat memperoleh perhitungan frekuensi pada variable
kategori melalui:
ArcToolbox>Analysis>Statistics>Frequency
1.3 Pearson
Product Moment Correlation Coefficient (r)
§
Mengukur derajat asosiasi atau kekuatan dari
hubungan antara dua variable kontinu
§
Skalanya bervariasi dari (–1
melalui 0 ke +1)
-1 mengisyaratkan hubungan
negatif sempurna
0 mengisyaratkan tidak ada
hubungan (asosiasi)
+1 mengisyaratkan hubungan positif
yang sempurna
Di mana Sx dan Sy adalah
standar deviasi dari X dan Y, dan X dan Y adalah mean.
2.
Statistik
Deskriptif Klasik: Bivariate
Rumus
Perhitungan untuk Pearson Product Moment
Correlation Coefficient (r)
Contoh
Koefisien Korelasi menggunakan “rumus perhitungan”
Ketika kita menelusuri statistik spasial, kita akan
melihat banyak analogi untuk mean, varians, dan koefisien korelasi, dan
berbagai formula mereka
3.
Statistik
Inferensial
§
Seringkali,
kita kekurangan data untuk seluruh populasi (semua kemungkinan kejadian)
sehingga sebagian besar ukuran (statistik) diperkirakan berdasarkan data sampel.
- Statistik
adalah ukuran yang dihitung dari sampel yang merupakan perkiraan parameter
populasi
§
Pertanyaan
harus selalu ditanyakan, apakah perbedaan yang diamati (katakanlah antara dua
statistik) bisa muncul karena peluang yang terkait dengan proses pengambilan
sampel, atau mencerminkan perbedaan nyata dalam populasi yang mendasari (s).
§
Jawaban
atas pertanyaan ini melibatkan konsep inferensi statistik dan pengujian
hipotesis statistik.
§
Signifikansi
statistik tidak selalu sama dengan signifikansi ilmiah (atau substantif).
- Dengan
ukuran sampel yang cukup besar (dan data
sets sering besar dalam GIS), signifikansi statistik sering mudah dicapai
4.
Pengujian
Hipotesis Statistik:
4.1 Pendekatan Klasik
§
Pengujian
hipotesis statistik biasanya melibatkan 2 nilai
§ Ukuran
atau indeks yang berasal dari sampel (misalnya pusat rata-rata atau Indeks
Tetangga Terdekat)
§ Statistik
uji, yang berasal dari ukuran atau indeks, yang distribusi probabilitasnya
diketahui ketika sampel berulang dibuat,
§ Ini
digunakan untuk menguji signifikansi statistik dari ukuran/indeks
§ Kita
melanjutkan dari hipotesis nol (Ho) bahwa dalam populasi, ada "tidak ada
perbedaan" antara dua statistik sampel, atau dari keacakan spasial (spatial randomness)
§
Jika
statistik uji yang kita peroleh sangat tidak mungkin terjadi (kurang dari 5%
kemungkinan) jika hipotesis nol itu benar, hipotesis nol ditolak
Jika statistik uji berada di luar +/-
1.96 (dengan asumsi distribusi Normal), kita menolak hipotesis nol (tidak ada
perbedaan) dan mengasumsikan perbedaan yang signifikan secara statistik
setidaknya pada tingkat signifikansi 0,05.
4.2 Pendekatan Simulasi
§ Karena
kompleksitas yang melekat pada proses spasial, kadang-kadang sulit untuk
mendapatkan statistik uji yang sah yang distribusi probabilitasnya diketahui
§
Pendekatan
alternatif adalah menggunakan komputer untuk mensimulasikan pola spasial acak
ganda (atau sampel) - katakanlah 100, statistik spasial (misalnya NNI atau
LISA) dihitung untuk masing-masing, dan kemudian ditampilkan sebagai distribusi
frekuensi.
- Distribusi
sampling simulasi ini kemudian dapat digunakan untuk menilai kemungkinan
memperoleh nilai yang kita amati untuk Indeks jika pola itu acak.
Statistik Centrographic
§
Deskriptor
dasar untuk distribusi titik spasial
§
Ukuran
Sentralitas
Mean Center
Centroid
Rata-rata pusat
tertimbang
Pusat Jarak
Minimum
§
Ukuran
Dispersi
Jarak Standar
Ellipse Deviasi
Standar
§
Dua
dimensi (spasial) setara dengan statistik deskriptif standar untuk distribusi
variabel tunggal
§
Dapat
diterapkan pada poligon dengan terlebih dahulu mendapatkan centroid dari
masing-masing poligon
§ Paling
baik digunakan dalam konteks perbandingan untuk membandingkan satu distribusi
(misalnya pada tahun 1990, atau untuk pria) dengan yang lain (misalnya pada
tahun 2000, atau untuk wanita)
Mean Center
§
Cukup
mean dari koordinat X dan Y untuk satu set poin
§
Juga
disebut pusat gravitasi atau centroid
§
Jumlah
perbedaan antara mean X dan semua X lainnya adalah nol (sama untuk Y)
§
Meminimalkan
jumlah jarak kuadrat antara dirinya dan semua titik
Centroid
§
Setara
untuk poligon dari pusat rata-rata untuk distribusi titik
§
Pusat
gravitasi atau titik balancing dari
polygon
§
Jika
poligon terdiri dari segmen garis lurus antara node, centroid diberi
"rata-rata X, rata-rata Y" dari node
§
Perhitungan
kadang-kadang diperkirakan sebagai pusat kotak pembatas
§
Dengan
menghitung centroid untuk satu set poligon dapat menerapkan Statistik
Centrographic ke polygon
Weighted Mean Center
(Pusat Rata-Rata Tertimbang)
§
Diproduksi
dengan membobot setiap X dan Y berkoordinasi dengan variabel lain (Wi)
§
Centroids
berasal dari poligon dapat ditimbang dengan karakteristik polygon
Pusat Jarak Minimum
(Center of Minimum Distance) atau Median Center
§
Juga
disebut titik minimum aggregate travel
Standard Distance
Deviation
§
Merupakan
standar deviasi dari jarak setiap titik dari pusat rata-rata
§
Rumus
untuk standar deviasi dari variabel tunggal
Analisis Pola Titik (Point Pattern Analysis)
Analisis sifat spasial dari seluruh tubuh poin
daripada penurunan ukuran ringkasan tunggal
Dua pendekatan utama:
§
Pendekatan
Titik Kerapatan menggunakan Analisis Kuadrat berdasarkan pengamatan/observasi
distribusi frekuensi atau kepadatan poin dalam satu set kotak grid.
-
Pendekatan
rasio varians/mean
-
Pendekatan
perbandingan distribusi frekuensi
§
Pendekatan
Titik Interaksi menggunakan Analisis Tetangga Terdekat berdasarkan jarak titik
satu dengan yang lain
Analisis Kuadrat: Variance/Mean Ratio (VMR)
§
Perlakukan
setiap sel sebagai pengamatan dan hitung jumlah titik di dalamnya, untuk
membuat variabel X
§
Hitung
varians dan mean X, dan buat varians untuk rasio rata-rata: varians/mean
ð
Untuk
distribusi seragam (uniform distribution),
variansnya nol.
Oleh karena itu,
kita mengharapkan rasio varians-mean mendekati 0
ð
Untuk
distribusi acak (random distribution), varians dan mean adalah sama.
Oleh karena itu,
kita mengharapkan rasio varians-mean sekitar 1
ð
Untuk
distribusi cluster (clustered distribution),
variasinya relatif besar
Oleh karena itu,
kita mengharapkan rasio varians-mean di atas 1
Rumus untuk varians :
§
Kelemahan
Analisis Kuadrat
- Hasil
mungkin bergantung pada ukuran dan orientasi kuadrat
Menguji berbagai
ukuran (atau orientasi) untuk menentukan efek dari setiap tes pada hasil
- Apakah
ukuran dispersi, dan bukan benar-benar pola, karena didasarkan terutama pada
kepadatan poin, dan bukan pengaturan mereka dalam kaitannya dengan satu sama
lain
- Hasil
dalam ukuran tunggal untuk seluruh distribusi, sehingga variasi dalam wilayah
tersebut tidak dikenali (dapat dikelompokkan secara lokal di beberapa area,
tetapi tidak secara keseluruhan)
Daftar Pustaka
Tim Pengampu SIG. 2007. Spatial Statistics. UPN
Veteran, Jawa Timur.
http://www.datakampus.com/2017/02/tendensi-sentral-mean-media-modus/.
Diakses Sabtu, 12 Mei 2018.









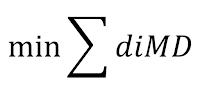





Komentar
Posting Komentar